[2024年更新:本文反映2021年的情況,因應最新法例,本文標題及部份內容經刪改,減低違法風險]
古語有云,“There are three kinds of lies: lies, damned lies, and statistics”,本文介紹一下有關 Simpson’s Paradox,以及在當局公布疫苗數據方面的例子。
Simpson’s Paradox
Simpson’s Paradox(辛普森悖論),簡單來說,就是若將性質不同的群組集合作整體統計(如所有年齡組別染疫的整體死亡率比較),得出的結論,可能與將群組分開統計(如按年齡組別列出死亡率比較)的結論,完全相反。「有心人」大可以按其動機,選取如何表達統計結果。
最新鮮的 Simpson’s Paradox 教科書例子,莫過於中國與意大利的新冠肺炎死亡率比較 [1]:
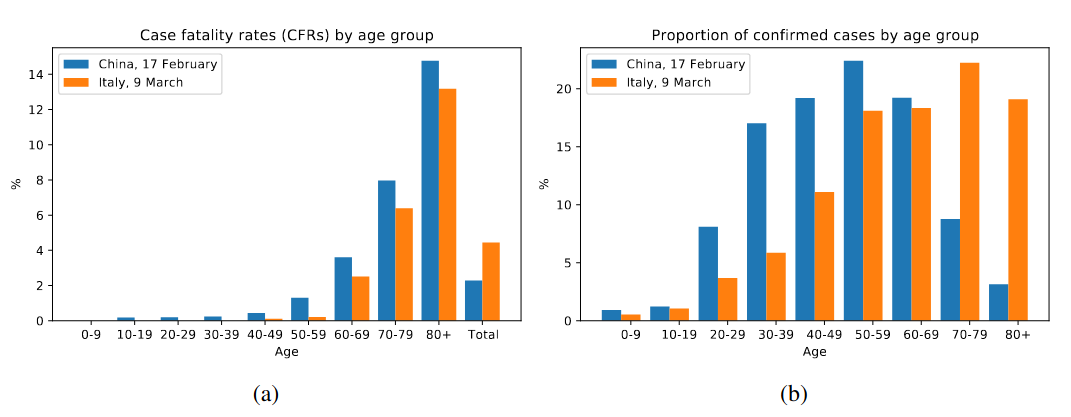
上圖 (a) 顯示 2020 年初,兩國按年齡分布的死亡率及整體死亡率(最右方 “Total” 一項)。可見若整體計算,中國死亡率(2.3%)比意大利(4.4%)低很多,但若分開以年齡組別計算,中國所有年齡組別的死亡率(除雙方均為 0% 的 0-9 歲組別)均高於意大利。
出現這現象的關鍵,是按年齡組別計算的染疫人口分布(上圖 b),當中統計涵蓋的中國染疫人口,較涵蓋的意大利染疫人口年輕得多(而這又源於兩國整體人口分布)。由於年輕人口染疫的死亡率較低,自然拖低了中國的整體死亡率。換句話說,雖然從任何一個年齡組別抽樣,在中國的死亡機會都高於意大利,但兩者的整體死亡率,還反映了年齡分布造成的差異。由於年齡是決定死亡率的重要因素,單是整體死亡率數字,是不能反映兩者的醫治水平的。
因此,若有人給你一些整體的數字比較,或許是嘗試引導你達到某些結論。這時便要格外留意,當中會否涉及因個案分布而導致兩者不能作有意義比較的情況。
個案:打針風險數據
在此看看當局在 2021 年 5 月 19 日的監測簡報會 [2] 公布,截至 5 月 16 日的懷疑涉及打針後出現嚴重異常事件數據及相關的「背景發生率」,和當局如何使用有關數據。
以下借用明報圖表 [3],顯示當局當時公布,是否打針以及相關的事故發生比率的比較。
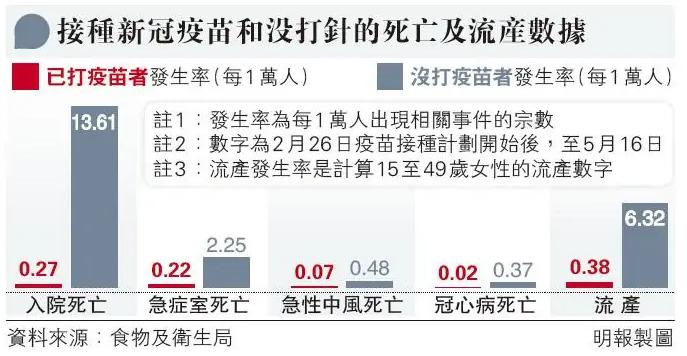
這些數據顯示,打針的事故發生率比不打針還低,食物及衛生局長副局長徐德義據此在簡報會指出,「根據上述數字的統計分析,未有證據顯示接種疫苗增加接種者的死亡或流產風險。」
據報同一場合,顧問專家委員會召集人劉澤星指,港大團隊檢視這些數據時,會分開性別和年齡組別,仔細分析病史,希望未來可更仔細交代,釋除疑慮 [4]。
明顯有違常理的比較
其實單看當局就有沒有打針這兩組整體事故比率的數字,已經很清楚,是不可作為疫苗風險的有意義比較,因為打肺炎針能大幅減低死亡及流產風險,根本不合常理(除非是重大發現)。問題原因,很可能就是類似上述 Simpson’s Paradox 的情況,即有打針和沒有打針的樣本,兩者組成分布存有顯著差異。
流產比率
先看「流產比率」。當局曾指出,復必泰疫苗的接種須知列明,「一般情況下,懷孕期間接種 2019 冠狀病毒病疫苗不是常規建議,除非有關女性被界定為有極高感染或在感染 2019 冠狀病毒病後有出現併發症的風險;懷孕或計劃懷孕的女性在接種復必泰疫苗前應徵求醫生意見」,而科興疫苗的接種須知則列明,「懷孕期間的婦女不應接種該款疫苗」。因此,可以預期,在已打針的 15 至 49 歲女士中,懷孕的比例應遠低於沒有打針的組別 [5]。
由於有懷孕才會流產,沒有懷孕分組流產比率是 0%。統計群組內沒有懷孕的比率高,必然拖低整體流產比率。因此打針後流產的(每一萬名15至49歲女士 0.38 宗)遠低於無打針的 6.32 宗的原因,很可能僅反映兩者樣本的懷孕比率差別,而不是疫苗與流產的關係。
在沒有進一步數據下,難以得出打針與流產風險之間的相關性,因為假使打針增加了流產風險,亦可能出現 Simpson’s Paradox,基於懷孕比率不同,出現同樣結果逆轉,即打針樣本的整體流產風險比率較低。
死亡率
上圖數據中的死亡率比較,均有類似情況。例如中風及心臟病的死亡比率,很可能和年齡或健康情況有關;若打針人口的較年輕或健康情況較佳,便會同樣令已打針樣本的死亡率較低。
為進一步驗証年齡分布,以下圖表比較已打第一針人口的年齡分布( 6 月 2 日下載),及 2020 年統計署的香港整體人口百份比分布。
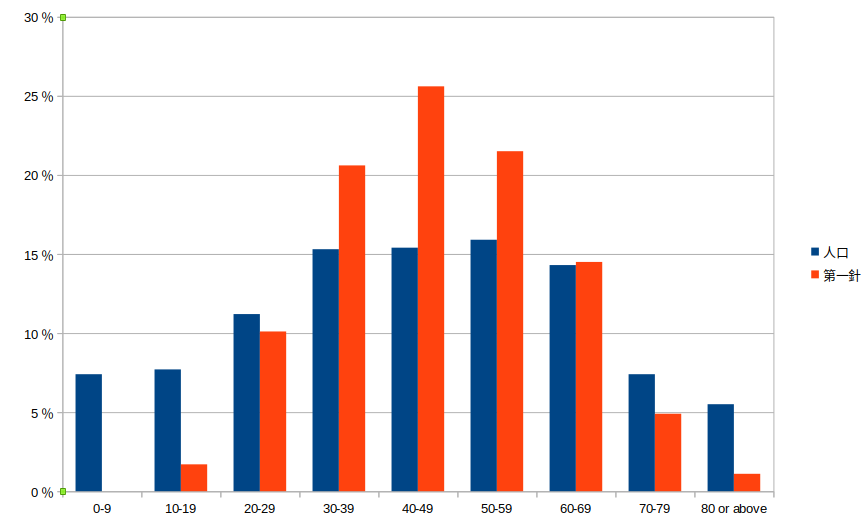
從圖表可見,已打針人口 70 歲以上的比率(6.0%),遠比整體人口 70 歲以上的比率(12.9%)為低(若改以 60 歲為界,因兩邊 60-69 歲比率相近,總百分比差距亦相若)。由於相信較高齡組別的中風及心臟病死亡比率,較其他組別高,再加上長期病患或三高人士,不論年齡,可能較不傾向打針;兩者的效果,均會大幅降低打針人口死亡的比率。
自我選擇偏差
從另一角度看,公眾最想知道的,是打針會否增加各項風險,最理想的方法,是有兩組人,其分布完全一樣(例如性別,年齡,健康情況),然後一組打疫苗,一組不打(更嚴謹的是打無效力的安慰劑,而參與者並不知自己打的是哪一類針,即疫苗第三階段臨床測試的雙盲做法),才可消除兩者的採樣偏差。而當局目前的做法,打針與不打針,都經過自我選擇,類似做統計的自我選擇偏差(Self-selection bias),以致 5 月 19 日的簡報會所公布的整體比較數據,對風險問題,可謂沒有什麼參考價值。
誤導性數據 x 誤導性陳述
當局固然不會不明白上述道理,因此才會給港大繼續按分組及病史分析數據,希望未來再交代。但同時,卻在有詳細分析前,其新聞稿卻列出兩組沒有比較意義的數字,再加一句按有關數據分析,「未有證據顯示接種疫苗增加接種者的死亡或流產風險」,技術上完全正確--由於單看兩組數字不足以作任何結論,因此說根據這些數字分析,未有證據顯示「X」,「X」填任何東西都沒有錯。但如此的統計數字及說法,大部份公眾聽來,很易理解為打針安全的正面證據。
之後,各建制傳媒及社交媒體,隨即洗版式重覆此論述。
這種「未有證據顯示 …」的句式,在沒有否定理據下,給人否定的感覺,很容易在潛意識下理解為否定。在並列的誤導性數據影響的之下,更容易出現這種理解。在報導上述訊息的媒體中,很多便偏離了官方訂下的表述。
訊息的傳播演化
如「添馬台」在其 Facebook 帖文 [6],以下為該帖文製圖:

圖中列出了有關數據,標題卻為「接種疫苗並沒有增加死亡或流產風險」,帖文內文並表示「看過全面的數據後,大家便不會被一些以偏概全的資訊誤導!」,更加上一個「#科學為本」的 tag。如上文解釋,單就所列的比較數據,僅可用官方「沒有證據」增加風險的說法,而不能肯定地說「沒有」增加風險。打着「#科學」的標簽,做了有違科學的示範,更將有問題的比較,說為全面的數據,對當局的質疑歸納為「以偏概全的誤導」[7]。
Simpson’s Paradox 的啟示,就是「全」不一定是周全,「偏」不一定是偏頗,整體比較的結果,在各組別之間有實質差異的時候,可以比分組比較更為誤導。
而港台新聞片段中 [8] 顯示,顧問專家委員會召集人劉澤星,在簡介會讀完數字後,也直接(可能不按稿)說了「沒有增加風險」;其後一些傳媒,如星島20日有關的標題 [9],亦為「打疫苗無添死亡中風等風險」。兩者與「添馬台」犯了同樣問題。
文匯報除了報導「無增死亡風險」,還貼心地給讀者計算,表列了未打針者的各項風險,比打針者高出多少倍( 5.8 至 49.4 倍不等),只差未直接說,接種能大幅減低死亡或流產風險 [10]。
即使一些另類的意見表達,如特首辦前新聞統籌專員,資深傳媒人何安達,指「政府在打針前已應公布相關數據,現時是『慢了很多拍』,他建議特首林鄭月娥及司長不應再呼籲打針,憂有反效果」以及「既然已整理出數據,政府應大事宣傳」,表面上挖苦領導,實際上卻也給這些數據背了書 [11]。
公眾吸收官方樂見的印象
經上述官媒,傳媒傳播,無論是有心無意以訛傳訛,久而久之,公眾吸收了的印象,很易演化成「數據證明疫苗安全」。如明報 6 月 1 日社評[12],便有如此表述「上月中,政府開始定期羅列流產、急性中風、心肌梗塞死亡等數據,顯示打針者相關出事率,全部較同期沒打針者低,證明疫苗安全」。諷刺的是,該社評正正在概嘆,市民對打針有焦慮,是「因為對事件不掌握,又或來自新聞報道的誤會錯誤觀念和印象」。這說明即使是對媒體操控高度警剔的傳媒中人,亦難以免疫,何況是一般受眾。
統一的旋律
面對這麼明顯有問題的數據,似乎少有專家、學者、傳媒發出不協和音,以至有意無意參與其傳播,是為鼓勵打針的目的而默許這些可誤導公眾的數據及說法,還是本身都被誤導了?
由自由撰稿人關偉基投稿, 5 月 25 日刊於明報的文章:《疫苗數據的疑惑》,是筆者所見唯一對數據提出同樣問題的文章,但畢竟只是滄海一粟。[2024年:明報連結已失效,文章仍可於 Internet Archive 查閱。]
如何破解 Simpson’s Paradox
要從兩組組成不同的樣本中,作有意義的比較,便須如當日指出,將兩邊按年齡及健康情況分組,每組分開比較,看看每組的打針與未打針數據的異常事故比率有否統計上的顯著分別。若要作整體比較,則至少要將其中一邊(如已打針)的數據,作分組加權調整 [13],使其與另一邊相同。當然,問題是,如何按健康情況分組可算合適,已有難度,加上當局應沒有具備已打針者或未打針者的健康情況資料,可能要進行另一項調查仲算。若只能以年齡分組,而每組的健康情差異無法消除,數據仍是無法有效比較。
聲明
為免引起誤解,在此強調,筆者並非任何醫療或傳染病學相關專業,本篇絕無質疑任何疫苗的安全性,亦絕無意影響任何人打針的決定。本篇僅旨在指出當局在發放防疫資訊的問題,而目的在於矯正該等問題,絕無意圖引發對政府憎恨。
順便介紹一下經典,對統計有興趣人士如 Bill Gates 推介過的 How to Lie With Statistics by Darrel Huff, 1954 年出版;其第一式,便是偏差的樣本(biased samples)。
[1] 出典:Simpson’s paradox in Covid-19 case fatality rates: a mediation analysis of age-related causal effects,Julius von K ̈ugelgen et al., https://arxiv.org/pdf/2005.07180.pdf
[2] 見政府 5 月 19 日新聞稿: 食物及衞生局副局長於2019冠狀病毒病疫苗接種監測簡報會開場發言
[3] 明報:政府:沒有證據顯示接種新冠疫苗增加出現死亡、急性中風死亡、心肌梗塞死亡 和流產等風險,5月20日
[4] 商台新聞: 政府專家強調接種疫苗後死亡及急性中風比率低,5月20日
[5] 見政府 4 月 15 日新聞: 流產個案沒證據顯示涉疫苗接種
[6] 見「添馬台」帖文: 【無證據顯示接種疫苗增加死亡/流產風險】
[7] 順帶一提,此帖態度與 OGCIO 帖文,將對「安心出行」開放源碼的要求,劃為「網上一知半解嘅言論」同出一轍,見「安心出行」開放源碼疑問拆解
[8] 港台新聞短片, 劉澤星稱接種疫苗後沒有增加整體死亡率或急性中風等,5月19日
[9] 星島網:專家委員會:打疫苗無添死亡中風等風險,5月20日
[10] 文匯報:有數據有真相 接種無增死亡風險,5月20日
[11] 明報: 何安達稱數據公布「慢幾拍」 促林鄭勿再籲打針,5月20日
[12] 明報社評: 全城谷針軟硬兼施 扭轉不願打針風氣,6月1日
[13] 可參考文章:Solving Simpson’s Paradox with Inverse Probability Weighting